BZOJ4033 [HAOI2015] 树上染色 [卡常/滚动优化树状背包dp]
这题教给了我很多人生经验...
Problem
有一棵点数为 N 的树,树边有边权。给你一个在 0~N 之内的正整数 K,你要在这棵树中选择 K 个点,将其染成黑色,并
将其他的 N - K 个点染成白色。将所有点染色后,你会获得黑点两两之间的距离加上白点两两之间距离的和的收益。
问收益最大值是多少。
Solution
基本思路:树状 dp,对每个边算贡献
然后 $f_{k,i,j}$ 代表以 $i$ 为子树的前 $k$ 个儿子,一共有 $j$ 个黑点的对答案的最大贡献
于是我们有方程:
$$f_{k,i,j}=max(f_{k-1,i,j-m}+f_{siz_s,s,m}+val_{i\rightarrow s})$$
$s$ 是 $i$ 的儿子。
看上去是 $O(n^3)$ 实际可以通过证明得知如果你好好取了 min 那就是 $O(n^2)$ 的。
第一维可以被滚动掉然后就可以进行 dp 了。
然而??
你认为你这就 A 了??
naive!!
按照这种方程写的复杂度是个假的
在链下的情况,复杂度会被卡成 $O(n^3)$然而洛谷并没有这组数据,BZOJ 有
不过如果你常数卡得优秀的话是可以卡过 BZOJ 的
比如下面这份代码:
// Code by ajcxsu
// Problem: color on the tree 2?
#include<bits/stdc++.h>
#define _rg register
using namespace std;
typedef long long ll;
const int N=2010, M=1e4;
int h[N], to[M], nexp[M], p=1;
ll W[M];
inline void ins(int a, int b, ll w) { nexp[p]=h[a], h[a]=p, to[p]=b, W[p]=w, p++; }
ll f[N][N];
int siz[N];
int n,tot;
void dp(int x, int fa) {
siz[x]=1;
int minx, miny;
for(int u=h[x];u;u=nexp[u]) if(to[u]!=fa) dp(to[u], x), siz[x]+=siz[to[u]];
for(int i=2;i<=siz[x];i++) f[x][i]=-1ll;
for(int u=h[x];u;u=nexp[u])
if(to[u]!=fa) {
minx=min(tot, siz[x]);
for(_rg int j=minx;j>=0;j--) {
miny=min(j, siz[to[u]]); // min值不在循环里取即可卡过
for(_rg int k=0;k<=miny;k++)
if(f[x][j-k]!=-1ll)
f[x][j]=max(f[x][j], f[x][j-k]+f[to[u]][k]+W[u]*k*(tot-k)+W[u]*(siz[to[u]]-k)*(n-tot-siz[to[u]]+k));
}
}
}
int main() {
scanf("%d%d", &n, &tot);
int u,v;
ll w;
for(int i=0;i<n-1;i++) scanf("%d%d%lld", &u, &v, &w), ins(u,v,w), ins(v,u,w);
dp(1,0);
printf("%lld\n", f[1][tot]);
return 0;
} 那么真正的方程是什么呢?
其实方程没变。
但你得正着转移。
下面是正确的 $O(n^2)$ 代码。
// Code by ajcxsu
// Problem: color on the tree 2?
#include<bits/stdc++.h>
#define _rg register
using namespace std;
typedef long long ll;
const int N=2010, M=1e4;
int h[N], to[M], nexp[M], p=1;
ll W[M];
inline void ins(int a, int b, ll w) { nexp[p]=h[a], h[a]=p, to[p]=b, W[p]=w, p++; }
ll f[N][N];
int siz[N];
int n,tot;
void dp(int x, int fa) {
siz[x]=1;
int minx, miny;
for(int u=h[x];u;u=nexp[u])
if(to[u]!=fa) {
dp(to[u], x);
minx=min(tot, siz[x]);
for(_rg int j=minx;j>=0;j--) {
miny=min(tot-j, siz[to[u]]); // j+k<=tot -> k<=tot-j
for(_rg int k=miny;k>=0;k--)
f[x][j+k]=max(f[x][j+k], f[x][j]+f[to[u]][k]+W[u]*k*(tot-k)+W[u]*(siz[to[u]]-k)*(n-tot-siz[to[u]]+k));
}
siz[x]+=siz[to[u]]; // siz应当该循环之后才更新。
}
}
int main() {
scanf("%d%d", &n, &tot);
int u,v;
ll w;
for(int i=0;i<n-1;i++) scanf("%d%d%lld", &u, &v, &w), ins(u,v,w), ins(v,u,w);
dp(1,0);
printf("%lld\n", f[1][tot]);
return 0;
} 在我们的假代码里面,我们转移到第 2 层,是往第 1 层找值转移过来。
2 的红色部分是可以被达到的,1 的黑色部分是可以被达到的。
但我们发现这样子转移,2 会从 1 的橙色(无效)部分做很多无效的比较操作。
而我们如果从 1 转移到 2,我们会省去这一部分无效的操作。
siz 即限制了这一层能够达到的部分。
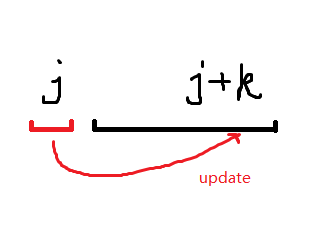
滚动的原理有些许的变化。
所处的 j 是上一层的旧状态,黑色的部分是已经被更新过的新状态。这就是我们为什么 j 仍然要从后往前枚举的原因。
同时,为了保证是从旧状态转移到新状态,k 也应从大到小枚举。
如果 k 从小到大,那么 j 会被最先更新,变成了用新状态更新新状态,答案会变大。
或者你将 k = 0 的情况另外处理,或把 j 的旧状态保存下来也行。
因此本题自始至终只有一种写法。
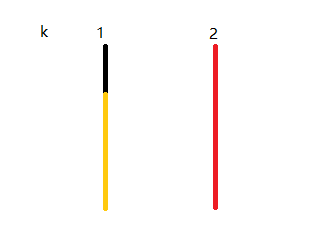
可以这样剪 if(n - k < k) k = n - k