ri 这题真 tm 难

Problem

JOI 村有一片荒地，上面竖着 N 个稻草人，村民们每年多次在稻草人们的周围举行祭典。
有一次，JOI 村的村长听到了稻草人们的启示，计划在荒地中开垦一片田地。和启示中的一样，田地需要满足以下条件：
田地的形状是边平行于坐标轴的长方形；
左下角和右上角各有一个稻草人；
田地的内部 (不包括边界) 没有稻草人。
给出每个稻草人的坐标，请你求出有多少遵从启示的田地的个数

Solution

先按 y 排序，然后对 x 分治。

很显然对分治出来的两半，左边的点都要在右边的点下面。
我们令上面的点为右上角，计算下面的点对上面的点贡献。

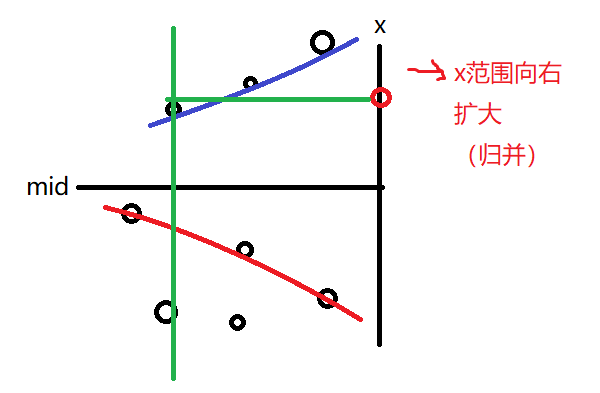
上面的点往后归并的同时，下方维护一个纵坐标递减的单调栈。

为什么要维护单调栈呢？由上图而知，红线下方的点是不能作为左下角的。

而若我们要计算红点的贡献，那么这个矩形能扩到的最左方是第一个纵坐标小于它的点。
如上图绿线所示。

所以我们只要维护上下方的单调栈，并且找出第一个纵坐标小于它的点的横坐标作为限制，对下方的单调栈的横坐标二分查找就行了。

Code

// Code by ajcxsu
// Problem: fakeman

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N=2e5+10;
struct Node {
    int x, y;
} nd[N];
bool operator <(const Node &a, const Node &b) { return a.x<b.x; }
bool cmp(const Node &a, const Node &b) { return a.y<b.y; }

ll tot;
Node ust[N];
Node dst[N];
int ut, dt;
void merge(int l, int r) {
    if(l==r) return;
    int mid=(l+r)>>1;
    merge(l, mid), merge(mid+1, r);
    ut=dt=0;
    int i=l, j=mid+1;
    while(i<=mid && j<=r) {
        if(nd[i].x<=nd[j].x) {
            while(dt && nd[i].y>dst[dt].y) dt--;
            dst[++dt]=nd[i];
            i++;
        }
        else {
            while(ut && nd[j].y<ust[ut].y) ut--;
            ust[++ut]=nd[j];
            tot+=dt-(lower_bound(dst+1, dst+dt+1, ust[ut-1])-dst)+1;
            j++;
        }
    }
    while(j<=r) {
        while(ut && nd[j].y<ust[ut].y) ut--;
        ust[++ut]=nd[j];
        tot+=dt-(lower_bound(dst+1, dst+dt+1, ust[ut-1])-dst)+1;
        j++;
    }
    inplace_merge(nd+l, nd+mid+1, nd+r+1);
}

int main() {
    int n;
    scanf("%d", &n);
    for(int i=1;i<=n;i++) scanf("%d%d", &nd[i].x, &nd[i].y);
    sort(nd+1, nd+1+n, cmp);
    merge(1,n);
    printf("%lld\n", tot);
    return 0;
}

本文链接：https://pst.iorinn.moe/archives/sol-bzoj-4237.html
许可： https://pst.iorinn.moe/license.html
若无特别说明，博客内的文章默认将采用 CC BY 4.0 许可协议 进行许可☆